C++ 递归详解

递归函数

在 C++ 中，递归函数是指在其定义体内调用自身的函数。以下是一个编写不当的递归示例：

#include <iostream>

void countDown(int count)
{
    std::cout << "push " << count << '\n';
    countDown(count - 1); // countDown 递归调用自身
}

int main()
{
    countDown(5);
    return 0;
}

当调用 countDown(5) 时，程序输出 push 5 并调用 countDown(4)；countDown(4) 再输出 push 4 并调用 countDown(3)。该模式持续，形成递归版的无限循环。

在《栈与堆》一课中，我们了解到每一次函数调用都会在调用栈上占用空间。由于 countDown 永不返回，这些信息永不被弹出，最终栈空间耗尽，产生栈溢出，程序崩溃或终止。在作者机器上，程序在崩溃前递减至 -11732。

作者注
尾调用（tail call）是指位于函数末尾的函数调用。带有尾递归的函数通常可被编译器优化为迭代形式，从而避免栈耗尽。若运行上述程序后发现其“永远”运行，极可能是编译器已执行此优化。

递归终止条件

递归函数与普通函数调用的最大差异在于：必须提供终止条件，否则将“无限”递归直至栈溢出。终止条件通常通过 if 语句实现。以下示例加入了终止条件与额外输出：

#include <iostream>

void countDown(int count)
{
    std::cout << "push " << count << '\n';

    if (count > 1)                // 终止条件
        countDown(count - 1);

    std::cout << "pop " << count << '\n';
}

int main()
{
    countDown(5);
    return 0;
}

运行结果：

push 5
push 4
push 3
push 2
push 1

此时栈内自顶向下为：

countDown(1)
countDown(2)
countDown(3)
countDown(4)
countDown(5)
main()

因终止条件，countDown(1) 不再调用 countDown(0)，而是输出 pop 1 后返回。随后各层依次返回并输出，最终得到：

push 5
push 4
push 3
push 2
push 1
pop 1
pop 2
pop 3
pop 4
pop 5

push 按正序输出（发生在递归调用之前），pop 按逆序输出（发生在递归调用之后，与出栈顺序一致）。

更具实用性的示例

以下函数递归计算 1 到 sumto（含）的整数和：

int sumTo(int sumto)
{
    if (sumto <= 0)
        return 0;      // 异常输入基线
    if (sumto == 1)
        return 1;      // 正常基线

    return sumTo(sumto - 1) + sumto; // 递归步骤
}

调用 sumTo(5) 的展开过程：

sumTo(5) → sumTo(4) + 5
sumTo(4) → sumTo(3) + 4
sumTo(3) → sumTo(2) + 3
sumTo(2) → sumTo(1) + 2
sumTo(1) → 1（基线）

回代：

sumTo(1) 返回 1
sumTo(2) 返回 1 + 2 = 3
sumTo(3) 返回 3 + 3 = 6
sumTo(4) 返回 6 + 4 = 10
sumTo(5) 返回 10 + 5 = 15

可见递归将问题分解为子问题，再组合子结果。

注意
代码使用 sumto - 1 而非 --sumto，以避免因副作用导致同一表达式多次使用变量时出现未定义行为。

递归算法

递归通常通过解决子问题来逼近原问题解。在上述算法中，sumTo(value) 先求 sumTo(value-1)，再加 value 得到最终答案。

多数递归算法对特定输入可直接给出答案（基线情况）。例如 sumTo(1) 直接返回 1，无需进一步递归。基线常对应输入 0、1、""、nullptr 等。

斐波那契数列

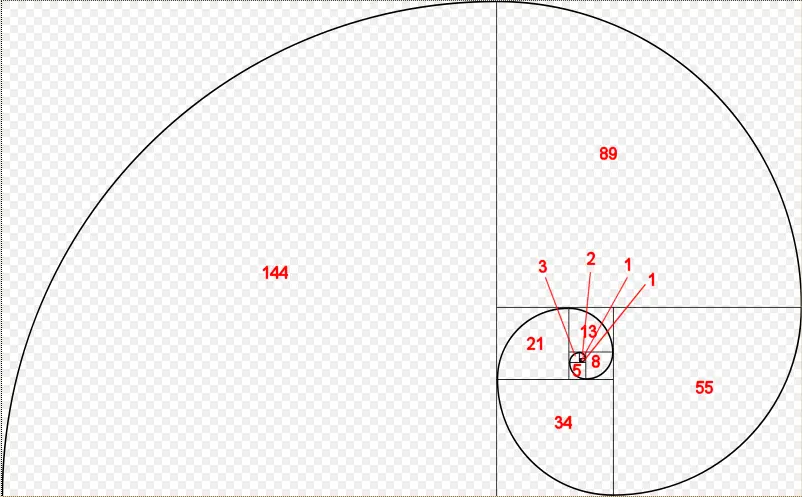
最著名的数学递归算法之一便是斐波那契数列。斐波那契数列广泛存在于自然界中，例如树木的分枝、贝壳的螺旋、菠萝的果眼、蕨类叶片的卷曲展开以及松果的排列等。下图展示了一个斐波那契螺旋： Code::Blocks安装

斐波那契数列在自然界中广泛存在，其数学定义为：

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)  (n > 1)

直接递归实现：

int fibonacci(int count)
{
    if (count == 0) return 0;
    if (count == 1) return 1;
    return fibonacci(count - 1) + fibonacci(count - 2);
}
int main()
{
    for (int count { 0 }; count < 13; ++count)
        std::cout << fibonacci(count) << ' ';

    return 0;
}

输出前 13 项：

0 1 1 2 3 5 8 13 21 34 55 89 144

记忆化（Memoization）

上述实现效率低下，因每次非基线调用均产生两次新调用，呈指数级增长（示例中调用 1205 次）。记忆化通过缓存已算结果避免重复计算：

#include <vector>

int fibonacci(std::size_t count)
{
    static std::vector<int> results{ 0, 1 };

    if (count < results.size())
        return results[count];

    results.push_back(fibonacci(count - 1) + fibonacci(count - 2));
    return results.back();
}

该版本仅产生 35 次调用，性能显著提升。

递归 vs 迭代

常见问题：“既然循环也能实现，为何使用递归？”

任何递归均可改写成迭代，但对非平凡问题，递归往往更简洁易读。
迭代通常更高效，因函数调用存在栈帧开销。
若递归实现清晰、维护性好，且递归深度可控、不在性能关键路径，则递归是合理选择。

适用递归的典型条件：

递归实现显著简洁；
递归深度受限，不会触发深层递归；
迭代实现需手动管理栈结构；
代码段对性能不敏感。

最佳实践：
通常优先使用迭代，除非递归更符合问题本质。

测验

编写递归函数 factorial，返回整数 N 的阶乘（0! = 1）。测试前 7 项。
（提示：连乘满足交换律，可自高向低递归。）
编写递归函数，输入正整数，返回各位数字之和（例：357 → 3 + 5 + 7 = 15）。验证 93427 → 25。

3-a) 编写程序，让用户输入正整数，并使用递归函数按方法 1（位逆序打印）输出其二进制表示。
（提示：递归调用后打印，即可逆序输出。）

3-b) （加分）扩展 3-a，处理 0 或负数输入，正确输出 32 位补码二进制。
（提示：无需处理负数本身，只要传入其对应无符号值即可得到正确位模式。）