以井字棋(Tic-tac-toe)为例,其标准棋盘为一个 3×3 的方格,两名玩家轮流在格内放置 “X” 和 “O”,率先连成三子者获胜。
虽然可以用 9 个独立变量来存储棋盘数据,但当存在大量同类元素时,数组更为合适:
int ttt[9]; // 一个包含 9 个整数的 C 风格数组(0 表示空,1 表示玩家 1,2 表示玩家 2)
该语句定义了一个顺序存储的 C 风格数组,元素在内存中排成一行:
// ttt[0] ttt[1] ttt[2] ttt[3] ttt[4] ttt[5] ttt[6] ttt[7] ttt[8]
数组的维度是指选取元素所需的下标数量。仅需一个下标的数组称为一维数组(1d 数组)。上例中的 ttt 即为一维数组,因为只需一个索引即可访问元素(如 ttt[2])。
然而,一维数组在视觉上与二维的井字棋盘并不相符。我们可以做得更好。
二维数组
在本章中我们提到,数组元素可以是任意对象类型,因此元素本身也可以是另一个数组。定义方式如下:
int a[3][5]; // 3 个元素,每个元素是包含 5 个 int 的数组
由数组组成的数组称为二维数组(2d 数组),因为它需要两个下标。
使用二维数组时,通常将第一个(左侧)下标视为行选择器,第二个(右侧)下标视为列选择器。概念上可将其排布为:
// 列 0 列 1 列 2 列 3 列 4
// a[0][0] a[0][1] a[0][2] a[0][3] a[0][4] 第 0 行
// a[1][0] a[1][1] a[1][2] a[1][3] a[1][4] 第 1 行
// a[2][0] a[2][1] a[2][2] a[2][3] a[2][4] 第 2 行
访问二维数组元素时只需使用两个下标:
a[2][3] = 7; // a[row][col],此处 row = 2,col = 3
因此,井字棋盘可定义为:
int ttt[3][3];
现在我们得到了一个 3×3 的网格,可通过行列下标轻松操作!
多维数组
维度超过一的数组统称为多维数组。
C++ 还支持三维及以上的多维数组:
int threedee[4][4][4]; // 4×4×4 数组(4 个数组,每个数组含 4 个数组,每个数组含 4 个 int)
例如,《我的世界》(Minecraft)的地形被划分为 16×16×16 的区块段(chunk sections)。
高于三维的数组同样受支持,但使用场景罕见。
二维数组在内存中的排布
内存本身是线性的(一维),因此多维数组在内存中需按顺序线性展开。
对于如下数组,有两种可能的存储方式:
// 列 0 列 1 列 2 列 3 列 4
// [0][0] [0][1] [0][2] [0][3] [0][4] 第 0 行
// [1][0] [1][1] [1][2] [1][3] [1][4] 第 1 行
// [2][0] [2][1] [2][2] [2][3] [2][4] 第 2 行
C++ 采用行优先(row-major order):元素按行依次连续存放,从左到右,自上而下:
[0][0] [0][1] [0][2] [0][3] [0][4] [1][0] [1][1] [1][2] [1][3] [1][4] [2][0] [2][1] [2][2] [2][3] [2][4]
某些其他语言(如 Fortran)采用列优先(column-major order):元素按列依次连续存放,从上到下,从左到右:
[0][0] [1][0] [2][0] [0][1] [1][1] [2][1] [0][2] [1][2] [2][2] [0][3] [1][3] [2][3] [0][4] [1][4] [2][4]
在 C++ 中,初始化数组时元素按行优先顺序赋值;遍历时若按内存顺序访问,效率最高。
二维数组的初始化
初始化二维数组最直观的方式是使用嵌套花括号,每一组数值代表一行:
int array[3][5]
{
{ 1, 2, 3, 4, 5 }, // 第 0 行
{ 6, 7, 8, 9, 10 }, // 第 1 行
{ 11, 12, 13, 14, 15 } // 第 2 行
};
尽管某些编译器允许省略内层花括号,我们仍强烈建议保留,以提升可读性。
使用内层花括号时,缺失的初始值将执行值初始化:
int array[3][5]
{
{ 1, 2 }, // 第 0 行:1, 2, 0, 0, 0
{ 6, 7, 8 }, // 第 1 行:6, 7, 8, 0, 0
{ 11, 12, 13, 14 } // 第 2 行:11, 12, 13, 14, 0
};
初始化多维数组时,可省略最左侧的维度长度:
int array[][5]
{
{ 1, 2, 3, 4, 5 },
{ 6, 7, 8, 9, 10 },
{ 11, 12, 13, 14, 15 }
};
此时编译器可根据初始值数量自动计算最左侧维度。非最左侧维度不可省略:
int array[][]
{
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 }
}; // 错误
与普通数组一样,多维数组可整体初始化为 0:
int array[3][5] {};
二维数组与循环
对一维数组,可用单循环遍历全部元素:
#include <iostream>
int main()
{
int arr[]{ 1, 2, 3, 4, 5 };
// 索引 for 循环
for (std::size_t i{0}; i < std::size(arr); ++i)
std::cout << arr[i] << ' ';
std::cout << '\n';
// 范围 for 循环
for (auto e : arr)
std::cout << e << ' ';
std::cout << '\n';
return 0;
}
对二维数组,则需两层循环:外层选择行,内层选择列。
同时需决定哪层循环在外,哪层在内。为按内存顺序访问,C++ 行优先,故行下标为外层循环,列下标为内层循环:
#include <iostream>
int main()
{
int arr[3][4]{
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 } };
// 双重索引 for 循环
for (std::size_t row{0}; row < std::size(arr); ++row) // std::size(arr) 返回行数
{
for (std::size_t col{0}; col < std::size(arr[0]); ++col) // std::size(arr[0]) 返回列数
std::cout << arr[row][col] << ' ';
std::cout << '\n';
}
// 双重范围 for 循环
for (const auto& arow : arr) // 取每一行
{
for (const auto& e : arow) // 取行内每个元素
std::cout << e << ' ';
std::cout << '\n';
}
return 0;
}
二维数组示例
看一个更实际的二维数组示例:
#include <iostream>
int main()
{
constexpr int numRows{ 10 };
constexpr int numCols{ 10 };
// 声明一个 10×10 数组
int product[numRows][numCols]{};
// 计算乘法表
// 第 0 行与第 0 列无需计算,因乘以 0 恒为 0
for (std::size_t row{ 1 }; row < numRows; ++row)
{
for (std::size_t col{ 1 }; col < numCols; ++col)
{
product[row][col] = static_cast<int>(row * col);
}
}
for (std::size_t row{ 1 }; row < numRows; ++row)
{
for (std::size_t col{ 1 }; col < numCols; ++col)
{
std::cout << product[row][col] << '\t';
}
std::cout << '\n';
}
return 0;
}
该程序计算并打印 1 到 9(含 1 与 9)的乘法表。注意打印时循环从 1 开始,以省略第 0 行和第 0 列,否则将输出大量 0。输出如下:
1 2 3 4 5 6 7 8 9
2 4 6 8 10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
笛卡尔坐标与数组下标
几何学中,常用笛卡尔坐标系描述对象位置。二维情况下,有两条坐标轴,传统命名为 “x” 与 “y”。x 为水平轴,y 为垂直轴。
二维平面内,物体位置可用 { x, y } 坐标对表示,分别指示该点距 x 轴右侧多远、距 y 轴上方多远。某些场景下 y 轴会反转,使 y 坐标表示距 y 轴下方多远。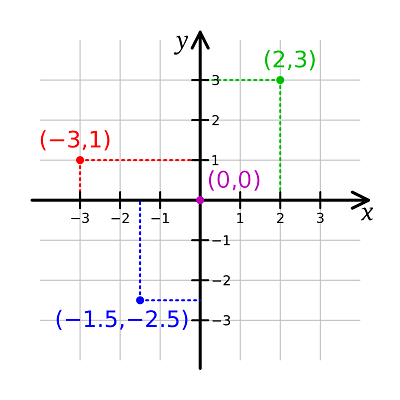
再看 C++ 二维数组的排布:
// 列 0 列 1 列 2 列 3 列 4
// [0][0] [0][1] [0][2] [0][3] [0][4] 第 0 行
// [1][0] [1][1] [1][2] [1][3] [1][4] 第 1 行
// [2][0] [2][1] [2][2] [2][3] [2][4] 第 2 行
这同样是一个二维坐标系,元素位置可用 [row][col] 描述(col 轴已反转)。
虽然两种坐标系各自易于理解,但从笛卡尔 { x, y } 转换到数组下标 [row][col] 却略显反直觉。
关键在于:笛卡尔 x 坐标对应数组列索引,y 坐标对应数组行索引。因此,笛卡尔 { x, y } 映射为数组 [y][x],与我们直觉中的字母顺序相反!
于是,二维循环常写成:
for (std::size_t y{0}; y < std::size(arr); ++y) // 外层循环为行 / y
{
for (std::size_t x{0}; x < std::size(arr[0]); ++x) // 内层循环为列 / x
std::cout << arr[y][x] << ' '; // 先 y(行),再 x(列)索引
}
注意此处数组索引为 a[y][x],与字母顺序相反,可能与您最初设想不同。
